PDDE-CONT

Note: PDDE-CONT has been superceded by Knut. The VFGEN command for PDDE-CONT is now unsupported, and it may be removed in a future version.

PDDE-CONT is a software package developed by Róbert Szalai for continuation and bifurcation analysis of periodic solutions to delay differential equations.

The VFGEN PDDECONT Command

A C++ system definition file for the PDDE-CONT package is created by the command

$ vfgen pddecont vector_field_file.vf

The vector field must have at least one delay expression.

Example 1

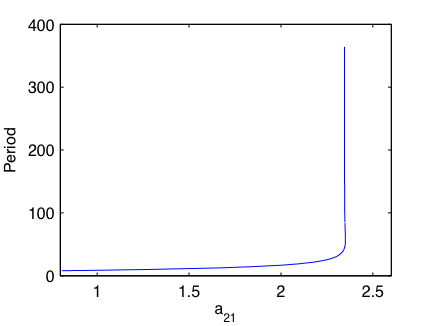
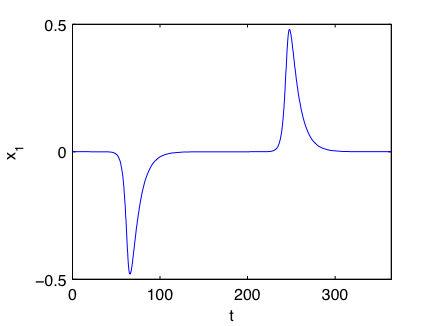
The file ShayerCampbell2000.vf defines the following system of equations:

x1'(t) = -κ x1(t) + β tanh(x1(t-τs)) + a12 tanh(x2(t-τ2))
x2'(t) = -κ x2(t) + β tanh(x2(t-τs)) + a21 tanh(x1(t-τ1))

This example was taken from the DDE-BIFTOOL manual. The reference given there for these equations is:

L. P. Shayer and S. A. Campbell. Stability, bifurcation and multistability in a system of two coupled neurons with multiple time delays, SIAM J. Applied Mathematics, 61(2):673-700, 2000.

The command

$ vfgen pddecont ShayerCampbell2000.vf
creates the file sys-ShayerCampbell2000.cpp.

This example uses these constants files:

The command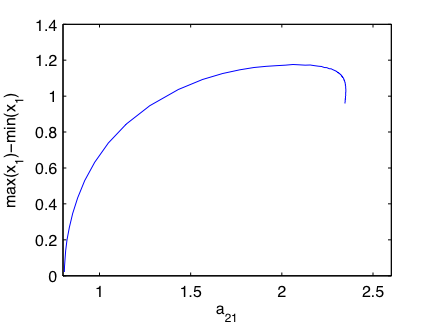
$ pdde -c cfile-ShayerCampbell2000-eq -o sc-eq.mat
computes a family of equilbria in which a Hopf bifurcation occurs. Then the next two commands compute the family of period orbits that arises at the Hopf bifurcation. The family is computed in two stages; during the second stage the number of discretization intervals is increased from 50 to 320.
$ pdde -c cfile-ShayerCampbell2000-po-a -i sc_eq.mat -o sc-po-a.mat
$ pdde -c cfile-ShayerCampbell2000-po-a -i sc-po-a.mat -o sc-po-b.mat
The following plots show max(x1)-min(x1) and the period of the orbits as a function of the parameter a21.
The family apparently converges to a homoclinic orbit. The following plot shows the graph of x1(t) of the last orbit computed.
(These plots were created in MATLAB, using the script scscript.m.)

Example 2

The equation

x '' + x + ε x ' + ε x3 = ε a cos(ω t )
is a second order weakly nonlinear periodically forced oscillator. In this example, we use PDDE-CONT to compute the resonance curve: the amplitude of the steady-state oscillation as a function of the forcing frequency ω.

The equation is not a delay equation; this example is simply a test of using PDDE-CONT to compute a family of solutions to a periodic vector field.

This equation can be written as the system

x '=y
y '=-x - ε y - ε x3 + ε a cos(ω t )
For convenience, we rescale time so that the period of the vector field is 1 by making the substitution
θ = ω t / (2π).

We obtain the system
x '(θ)=Ty
y '(θ)=T [-x - ε y - ε x3 + ε a cos(2π θ )]
where
T = (2π) / ω
A vector field file for this system is wn2.vf. We have set the default values of the parameters to ε = 0.1, a = 5, and T = 2π (which corresponds to ω = 1). An approximate periodic solution to this system is
x=1.85 cos(θ - 0.34)
y=1.79 cos(θ + 1.2)
(This was found by solving the system with an initial value solver, and adjusting the amplitudes and phases of the approximate solution until a visual comparison of the approximate solution and the numerical solution looked close.)

We create a system definition file for PDDE-CONT with the command

$ vfgen pddecont wn2.vf
This creates the file sys-wn2.cpp. We edit this file and add the approximate solution in the function sys_stsol: sys-wn2-edit.cpp.

We use the constants files

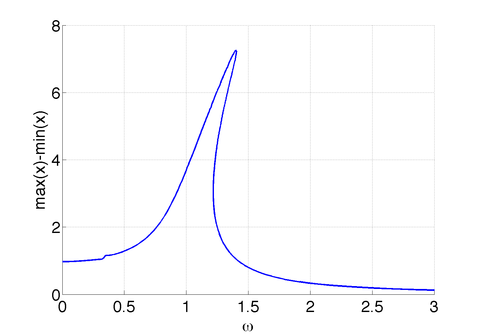
to compute the family of periodic orbits with the commands
$ pcompile sys-wn2-edit.cpp
$ pdde -c cfile-wn2a -o wn2a.mat
$ pdde -c cfile-wn2b -o wn2b.mat
$ pdde -c cfile-wn2c -i wn2b.mat -o wn2c.mat

The first pdde command computes the curve for T < 2π (ω > 1); the second and third pdde commands compute the curve for T > 2π (ω < 1).

Finally, we use the MATLAB script wnplot.m to create the following graph of the amplitude of the periodic orbit as a function of ω.